With Entanglement, Quantum Superposition is one of the cornerstones of quantum computing. It forms the basis of all quantum algorithms and is the main reason quantum computers can outperform classical computers on certain problems.
In this article, you will learn the origin of Superposition in the context of quantum mechanics, how it is used in various Quantum Algorithms, and why it is the reason quantum computing was thought up in the first place.
Enjoy!
What is Superposition?
Towards the end of the 19th and the beginning of the 20th century, physicists noticed that very small (sub-atomic) particles behaved rather oddly compared to the objects we know from our everyday lives. The theory they devised to explain these phenomena was called quantum mechanics and forms the basis of quantum computing.

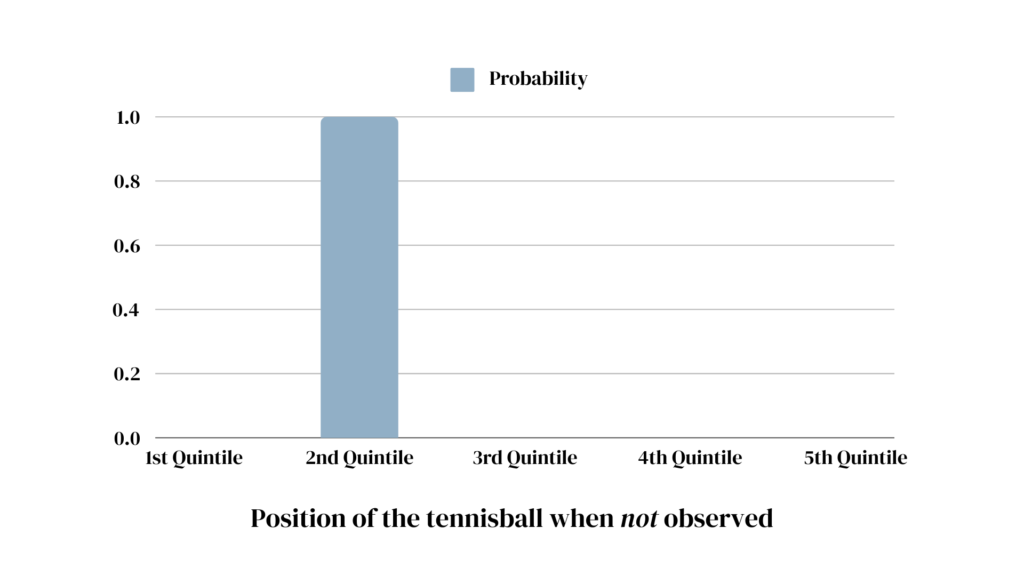
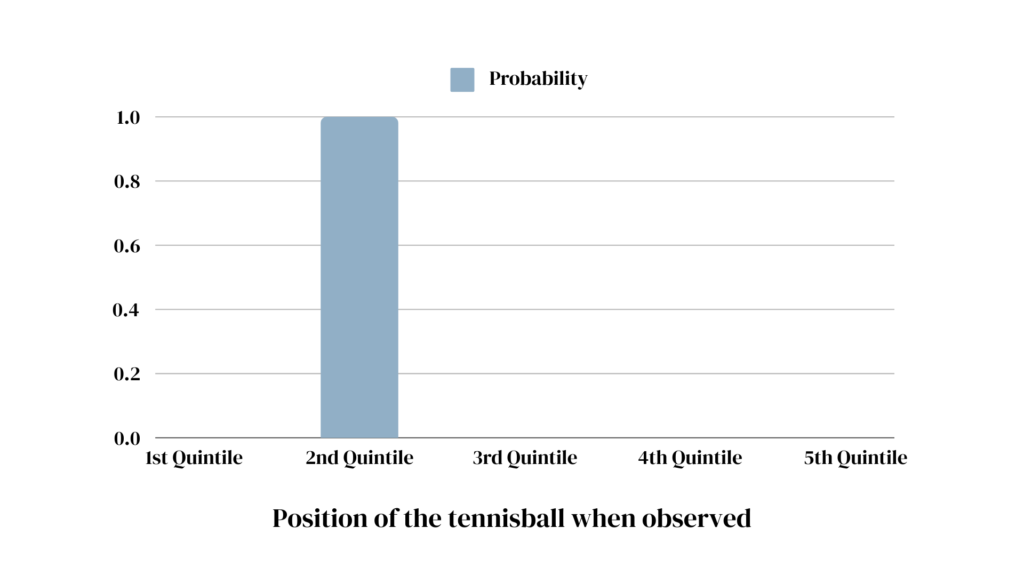
Let’s imagine a tennis ball in a glass tube. Whenever we look at it (observation), we can make a statement about its position. Even if we are not looking, we can be certain that the tennis ball is located at one precise point in the tube. Just because we don’t know where it is, doesn’t mean that it’s everywhere.
With quantum particles, things are not quite as easy.
Unless observed, the properties of quantum particles such as electrons exist in a probability distribution* of all possibilities. Only once we take a look (make an observation), does the probability distribution “collapse” and we find the electron at one distinct location.
* Technically speaking, we are not dealing with a probability distribution but a distribution of probability amplitudes. Unlike the probabilities we are used to from blackjack or roulette, probability amplitudes can also take on negative and complex values. Where this distinction comes from, is a whole different story…
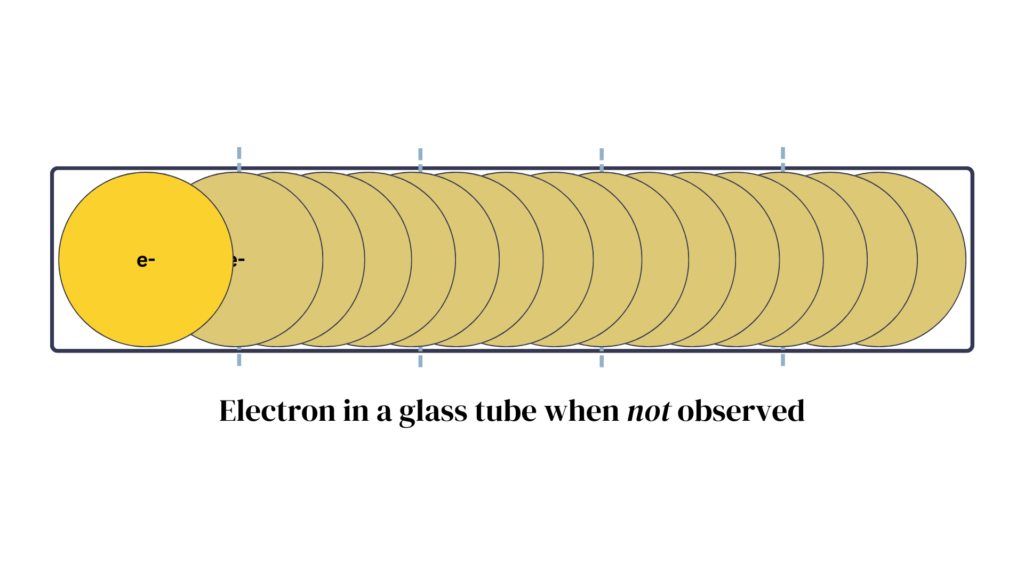
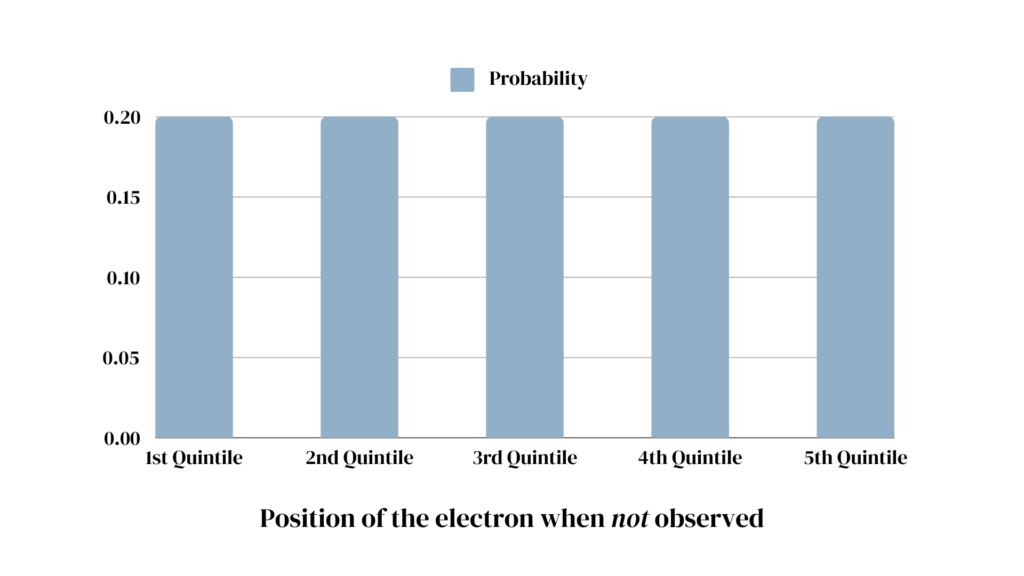
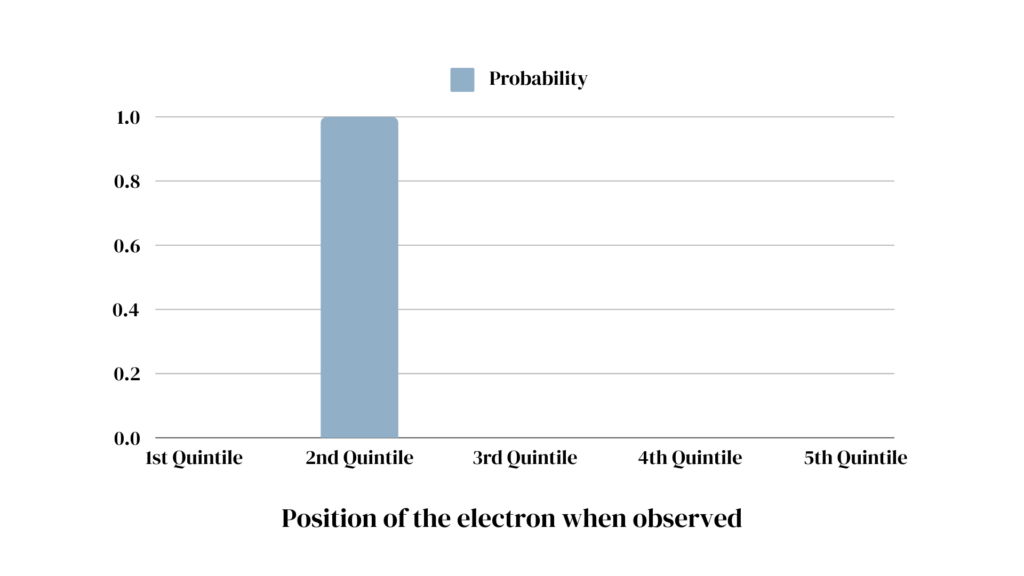
The important difference: In the tennis ball example, unless we look, we have to treat the ball’s location as a probability distribution. Although the ball is in one precise spot at a time, the best we can do is guess due to our lack of knowledge. If the tube is slightly tilted, for example, the ball is more likely to be located towards the lower end, but without further information, we still don’t know where exactly.
In the case of quantum mechanics, however, until we observe it, the electron exists in a probability (amplitude) distribution of all possible positions. To the best of our current understanding of quantum mechanics, the probability distribution is its state.
This phenomenon is referred to as Superposition and can occur for other quantum mechanical properties as well. Just like an electron can be in multiple positions at once (with a certain probability), it can also spin in the left and the right direction with a certain probability.
Why do we need a new kind of computer for this?
When Richard Feynman proposed the concept of a computer based on quantum mechanical phenomena in 1981 (s. Simulating Physics with Computers), it wasn’t to solve optimization problems or perform unstructured database search. Back then, his main concern was to efficiently simulate quantum mechanical systems such as medical drugs or chemical compounds. But why do we need a new type of computer for this?
Thinking back at our tennis ball example, a tennis ball can spin either to the right or the left*. It can be in either a state of r (for right) or l (for left). To describe the tennis ball, we only need to record one letter disclosing its spin direction.
* For now, let’s ignore the case of a non-spinning tennis ball in order to maintain the analogy to a binary system.
With more tennis balls, come more possible spin combinations.
If our system consists of two tennis balls, the possible states of the system are: rr, rl, lr, ll. Since our system is in one of these states at any point in time, we can describe it using two letters, one for the first and another for the second tennis ball.
For N tennis balls, we need to record N letters. In the quantum realm, things aren’t as simple…
Instead of a tennis ball, let our system consist of an electron. Like the tennis ball, this electron can spin to the right or to the left*.
*Physically speaking, the “spin” we are talking about here works a bit differently than the spin from our tennis ball example. For an explanation of the concept of spin in the quantum mechanical sense, see What is Quantum Mechanical Spin? by the Youtube channel Veritasium.
Unlike the tennis ball, however, the electron can also be in a Superposition of the two states. As a consequence, we can no longer describe the state of our 1-element system with a single letter. To account for the possibility of Superposition, we have to represent the state of our system using two numbers, \(\alpha\) and \( \beta\), each describing the probability (amplitude) of each spin direction:\( \alpha r + \beta l \).
If our system consists of two electrons, each in a potential Superposition state of r and l, we can describe it as \(\alpha rr + \beta rl + \gamma lr + \delta ll\). In total, we need \(2^2 = 4\) numbers to represent a two-element system. One for the probability (amplitude) of each pair of electron states.
To record the state of a system with N electrons, we need to keep track of \(2^N\) probability (amplitudes). For any additional electron, we need to note down twice as many spin combinations. In other words, a linear growth in the amount of elements is met with an exponential growth in the amount of information we need to keep track of.
…at least with a classical computer.
In a quantum computer, each quantum bit (qubit) is realized using an actual quantum property such as electron spin. Unlike classical bits, qubits can therefore be in the Superposition states we wish to simulate. For a quantum system with 30 (binary) properties, we can use 30 qubits instead of the \(2^30 = 1073741824\) numbers we would have to keep track of with a classical computer.
How can we use Superposition?
The last section covered how quantum computing originally emerged from the cradle of quantum mechanics. Back then, these considerations were ideas, purely theoretic. By now, (small-scale noisy) quantum computers have been built. Algorithms were developed that do not have the simulation of quantum mechanical systems as a goal, yet significantly outperform even the best classical (non-quantum) algorithms.
While a classical computer processes one data point from start to finish, through the use of Superposition, a quantum computer can manipulate the distribution of possible states with a single operation. This is sometimes referred to as Quantum Parallelism. (Have a look at my other article Is Quantum Computing really parallel? for a more in-depth discussion on why quantum computing should or should not be considered parallel.)
Grover’s Algorithm, for example, makes use of this idea. It begins by initializing a computer in an equal Superposition state of all possible inputs to a problem. Think of all the possible number sequences in a sudoku, for example. Each possibility is considered equally likely.
Then, an oracle function marks the state within the Superposition that provides a valid solution to the original problem. Since an operation applied to a Superposition state affects all of its component states, a single application of the oracle function is enough to evaluate all possibilities.
See How does Grover’s Algorithm work? for more context and details on the algorithm and where its quantum advantage comes from.
Summary
Whenever a quantum mechanical property or system (or a quantum computer for that manner) is in Superposition, its state can be seen as a probability (amplitude) distribution over multiple state values. Although quantum computing was originally conceived to efficiently simulate quantum mechanical systems, multiple quantum algorithms have been proposed for various domains that could outperform even the best classical (non-quantum) algorithms.
An operation applied to a system in Superposition can affect all component states of the Superposition. Thereby, although certain caveats apply, Superposition enables us to manipulate multiple values at once.