What is Phase Kickback?

Phase Kickback is a building block of many popular quantum algorithms, including Deutsch’s Algorithm, Quantum Phase Estimation, and Shor’s Algorithm for integer factorization. It is built on the mathematical notion of eigenvalues and eigenstates and enables us to reverse the chain of cause and effect (to some extent).

This article covers the basics of Phase Kickback, where it comes from mathematically, and how it can be used to extract information from operators of arbitrary size. Stay tuned!

Background and Examples

The eigenstates (aka. eigenvectors) of a matrix are all the vectors that when transformed by the matrix maintain their direction.

In other terms: \( M \vec{v} = \lambda \vec{v} \)

For a geometric introduction to the topic of eigenvectors and eigenstates, I recommend Grant Sanderson’s video on the matter: Eigenvectors and eigenvalues.

In the circuit model of quantum computing, every operation (= gate) we apply corresponds to a unitary matrix. If this matrix is applied to a qubit whose state is one of the eigenstates of the operator, the qubit’s state remains unaffected except for the scaling factor \lambda, further referred to as phase.

Let’s take the Z-gate as an example.

\(Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\)

Both pure states, |0> and |1> are eigenstates of the Z-operator with the corresponding eigenvalues of 1 and -1.

\(Z |0> = |0> \)

\(Z |1> = -1 \times |1>\)

So far, so good, but what happens when we apply the controlled version of the gate to a qubit in one of its eigenstates?

\( CZ * (X \otimes X) |00> = CZ |11> = – 1 \times |11> \)

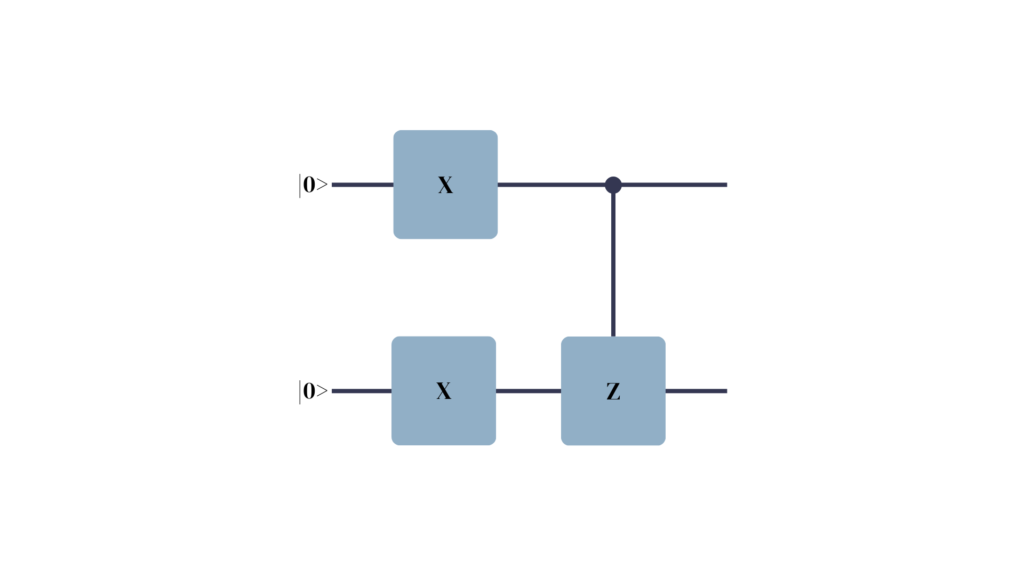
Since the second qubit is in a state of |1>, one of the eigenstates of the Z operator, the state remains unaffected by the operation except for a phase factor of -1. If we were to measure the system now, this phase factor would be lost. Upon measurement probability amplitudes are squared (s. Born’s rule) and |11> would be returned as the system state.

So, if phase factors can be factored out and vanish in the end, why should we care about them at all?

Let’s take a look at another example, one similar to the previous circuit except for its use of superposition, introduced through the use of a Hadamard gate:

\(|s0> = |00>\)

\(|s1> = \frac{1}{\sqrt{2}} (|00> + |10>)\)

\(|s2> = \frac{1}{\sqrt{2}} (|01> + |11>)\)

\(|s3> = \frac{1}{\sqrt{2}} (|01> + (-1) \times |11>) = \frac{1}{\sqrt{2}} (|0> – |1>) \otimes |1> = |-1>\)

\(|s4> = |11>\)

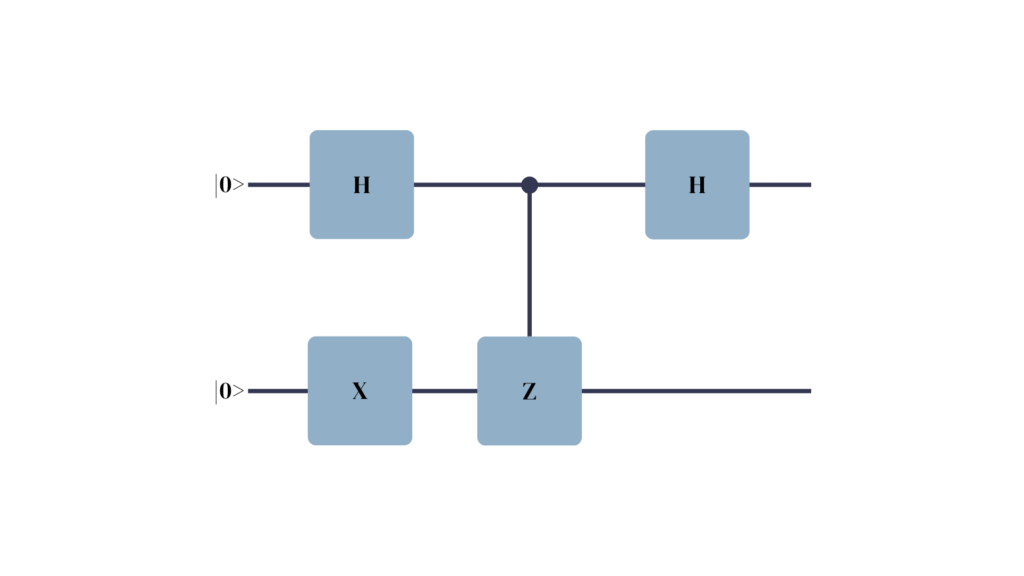
Even though we used a rather simple circuit to show it, what happened here marks the cornerstone of many essential quantum algorithms: Phase Kickback.

Although we applied the Z gate to the second qubit, we ended up affecting only the state of the control qubit. Through Phase Kickback, we were able to change the order of cause and effect.

The main difference between the first and the second circuit illustrates the difference between global and relative phase. In the first circuit, the phase factor is applied to the whole state (global phase). As such, the phase can be factored out and is lost upon measurement.

In the second circuit, the phase factor is applied to only one of the component states of the superposition (relative phase). The relative phase difference within the superposition state changes the result upon measurement.

Application

Throughout the years, Phase Kickback has found its way into many quantum algorithms as it enables us to extract the eigenvalue(s) of an arbitrarily large matrix into a single control qubit. Even if an operator acts on multiple qubits at once, the operator’s eigenvalue can still be kicked back to a single control qubit, as long as the target qubits are in the corresponding eigenstate of the operator.

The examples above were rather trivial in that we had to already know the eigenstates of the operator to be able to place the target qubits in the desired state. Things get more interesting when we treat the operator as a black box for which we know aspects of its behavior but not its implementation.

Deutsch’s algorithm is an example of such a situation. Although we do not know the nature of a provided function, from its postulated behavior we can derive the eigenstates and eigenvalues for each of the possibilities. This knowledge can then be used to distinguish types of possible implementations based on the phase factors they “kick back”.

If you are interested in learning the details of David Deutsch’s algorithm, the first algorithm to showcase the superiority of quantum computers, feel free to have a look at my other article: How does Deutsch’s Algorithm work?

Summary

Phase Kickback is a phenomenon that occurs in quantum computing whenever we apply a controlled gate to one of its eigenstates. It is based on the notion of eigenvalues and eigenstates and allows us to reverse the order of cause and effect, regardless of the size of the applied operator. To have a measurable effect, though, the control qubit must be in a state of superposition.