How does Grover’s Algorithm work?
Grover’s Algorithm is one of the most popular quantum algorithms. While it does not achieve the exponential speedup of Shor’s algorithm, it enables the user to find an entry in an unsorted list of N elements in only \(\sqrt{N}\) steps. The application areas of the algorithm range from speeding up database systems to solving problems with multiple possible solutions that are easy to verify but hard to find.
In this article, you will learn the core ideas behind Grover’s Algorithm, what kind of problems it can be applied to, and what we can learn from Grover’s Algorithm about quantum algorithm development in general.
The Problem
In Grover’s original paper as well as in most articles on the web, the problem that the algorithm solves is referred to as “Unstructured Database Search”. Let’s break this down to see what each term means in this context.
Database
A Database in this context is nothing more than a list of entries. These entries can be anything, from the name number pairs found in a phone book to all possible solutions of a crossword puzzle to every possible number distribution in a sudoku. For now, neither the shape nor the meaning of these entries matters much. A database is just a list of items.
Search
The overall goal of Search is to find an entry among a list of possibilities that has some useful characteristics. If our database is a phone book, we might want to find the name to a number that tried to call us before. If our database is a list of all possible solutions to a sudoku, our goal might be to select a valid solution given the rules of the game. Search means we want to find something.
Unstructured
Unstructured refers to the fact that the order of database entries is completely random. There is no inherent structure an algorithm could use to speed up the search. In contrast, if the database were sorted alphabetically, we could speed up the search for a word by repeatedly cutting the list in half and evaluating the entries at the intersection.
Since our database is assumed to be unstructured, the best any classical algorithm can do to find an entry is to go through the full list, one by one, and evaluate each entry individually. In the worst case, a list with N items would require us to perform N evaluations. Let’s find out how Grover managed to beat that.
The Solution
Grover’s Algorithm begins by creating an equal superposition of all available qubits. The resulting state can be seen as a uniform distribution over all possible entries. If we were to measure now, every entry would be equally likely, each with a probability of \(\frac{1}{N}\).
This step is common among many quantum algorithms such as Deutsch’s Algorithm or Shor’s Algorithm.
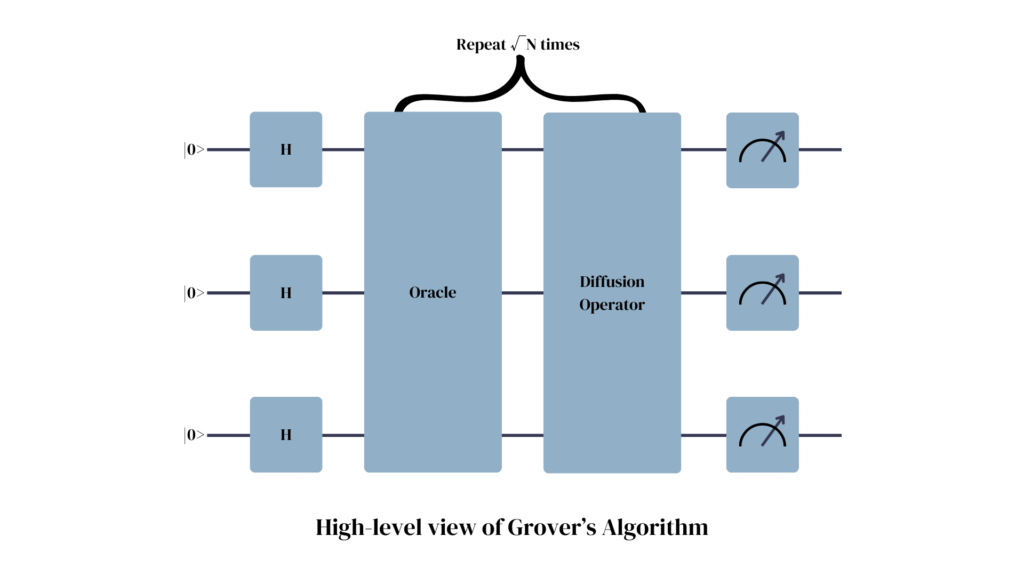
Next, an oracle function is applied that marks the desired state with a phase value of -1. While Grover’s Algorithm expects the oracle to behave in this way, how to implement it is not specified by the algorithm itself. The structure of the oracle depends on the problem we are aiming to solve.
The oracle function for finding the solution to a sudoku puzzle might look very different from the oracle function of a phone book database. As long as the oracle multiplies the probability amplitude of the targeted state by -1, the algorithm will work.
Finally, the Diffusion Operator is applied. After the oracle has been applied, the state of the system contains the information of which entry in the superposition is the desired outcome. However, we cannot simply return this entry.
If we were to measure the system, the factor of -1 that distinguishes the target state from its alternatives would be lost. It would not show in the resulting probability distribution. Upon measurement, probability amplitudes are squared (according to Born’s rule).
To extract the marked entry, we need an operator that corresponds to a unitary matrix AND increases the probability of the marked state while also reducing the probabilities of all other states (since total probability must sum to 1). Grover’s Diffusion Operator is such an operator.
Steps 2 and 3, the application of the oracle function and the Diffusion Operator, have to be repeated \(\sqrt{N}\) steps. (For a mathematical proof of this statement, I recommend a look at the original paper: A fast quantum mechanical algorithm for database search.)
In the next chapters, I will cover each of these components in more detail as well as some of the questions I had when first learning about Grover’s Algorithm.
The Oracle
The core idea of the oracle formalism in quantum computing is that of an exchangeable black box. As long as the oracle operator behaves a certain way, it does not matter how it is implemented. Algorithms that incorporate an oracle, can be applied to multiple problems of a similar nature. In Grover’s case: if a solution can be found classically by iterating over all of the possibilities and a found solution can be verified easily, Grover’s Algorithm can be applied.
While we know how the oracle in Grover’s Algorithm must behave, how to construct such an oracle for a new problem is likely going to be a high-regarded question once physical quantum computers reach industry adoption. The following graphic shows the trivial example of an oracle circuit and its corresponding unitary matrix for marking the |101> state in a 3-qubit system.
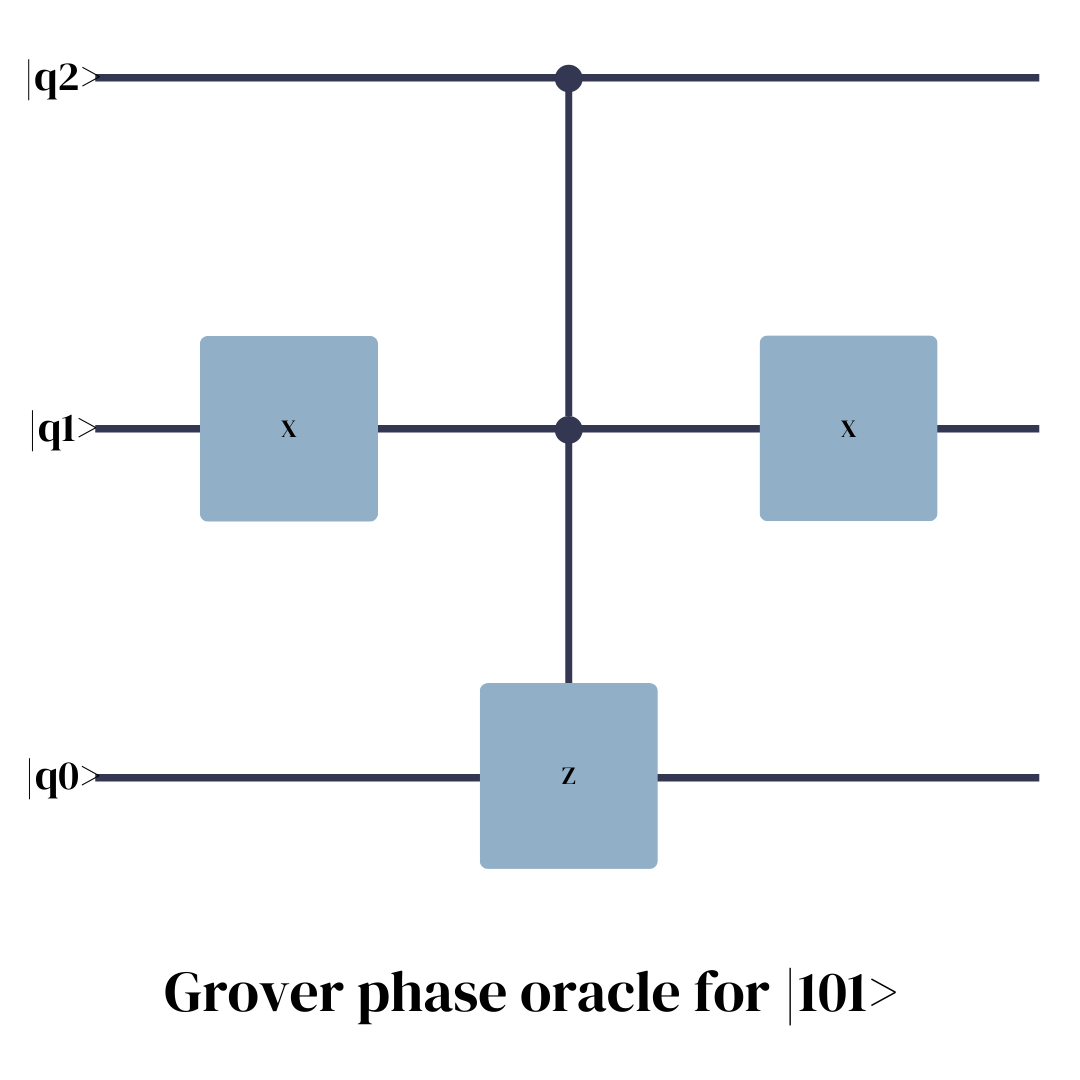
As we can see in the unitary matrix of our oracle, any state other than |101> is multiplied by a factor of 1. Only |101> is treated differently and receives a factor of -1. If the oracle modifies the previous superposition state, only the coefficients of the target state change.
This is one of the challenges in understanding Grover’s Algorithm (and quantum computing in general): If we already know what a correct solution looks like when constructing the oracle, what do we need the algorithm for?
Recognizing a correct solution when we see it is quite different from finding it in the first place. In a sudoku, verifying whether a solution is correct is easy. Check if each row, each column, and each square contains the numbers from 1 to 9 exactly once. If that is not the case, the proposed solution is incorrect. Checking a solution against a set of criteria is easy, finding it amongst the multitude of possible solutions is hard.
Furthermore: If our oracle function evaluates each state individually, how do we achieve a speedup compared to the brute force approach a classical computer would require?
Here lies the crux of superposition. While a superposition state can be viewed as a combination of individual states, it is a valid state in itself. When an operation (aka. a gate) is applied to a superposition state, it affects the coefficients of all the states comprising the superposition due to the linear nature of quantum computing. It is distributed among the individual states.
\(O(|0> + |1>) = O|0> + O|1>\)This is what is often referred to as Quantum Parallelism.
While affecting multiple states through a single operation seems fantastic at first, it is important to note that the same quantum mechanical principles that enable such fantastic feats also limit us in the operations we can perform: Every operator we wish to apply to a quantum state must correspond to a unitary matrix.
That’s why we cannot simply set the probability amplitude of the desired state to 1 and all others to 0. The corresponding operation would not be unitary!
To extract the marked state, Grover suggested his Diffusion Operator.
The Diffusion Operator
As mentioned in the previous section, each operation applied in a quantum computer must correspond to a unitary matrix. Lucky for us (and him), Lov Grover found an operator that is unitary, easy to interpret, and able to amplify the probability amplitude of a marked state while reducing the amplitudes of all other states.*
* Beyond the unitary matrix, there is a nice geometric interpretation for the Diffusion Operator using inversion about average. Here’s a good introduction video from the University of Chicago: https://www.youtube.com/watch?v=YEI5vYdcoQ4
This operator behaves differently, depending on the sign of each state in the superposition. The following figure shows a possible implementation of the Diffusion Operator for a 3-qubit system along with its unitary matrix:
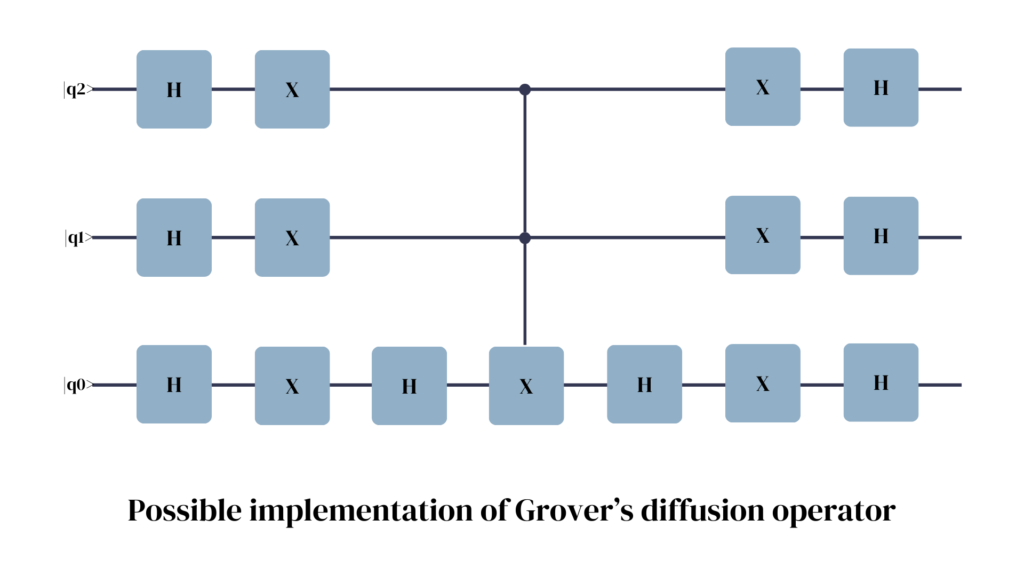
If the oracle marked a state, which therefore has a probability amplitude with a negative sign, its probability amplitude is enhanced. The amplitudes of all other states are reduced. After one iteration, the updated state of the 3 qubit system with the target state |101> is:
\( D \frac{1}{2\sqrt{2}} (|000> + |001> + |010> + |011> + |100> – |101> + |110> + |111>)\) \( = \frac{1}{2\sqrt{2}} (D |000> + D |001> + D |010> + D |011> + D |100> – D |101> + D |110> + D |111>) \) \(= \frac{1}{2\sqrt{2}} ((- 0.75 |000> + 0.25 |001> + 0.25 |010> + 0.25 |011> + 0.25 |100> + 0.25 |101> + 0.25 |110> + 0.25 |111>)\) \(+ (0.25 |000> + -0.75 |001> + 0.25 |010> + 0.25 |011> + 0.25 |100> + 0.25 |101> + 0.25 |110> + 0.25 |111>)\) \( + (0.25 |000> + 0.25 |001> – 0.75 |010> + 0.25 |011> + 0.25 |100> + 0.25 |101> + 0.25 |110> + 0.25 |111>)\) \( + (0.25 |000> + 0.25 |001> + 0.25 |010> – 0.75 |011> + 0.25 |100> + 0.25 |101> + 0.25 |110> + 0.25 |111>) \) \(+ (0.25 |000> + 0.25 |001> + 0.25 |010> + 0.25 |011> – 0.75 |100> + 0.25 |101> + 0.25 |110> + 0.25 |111>)\) \( + (- 0.25 |000> – 0.25 |001> – 0.25 |010> – 0.25 |011> – 0.25 |100> + 0.75 |101> – 0.25 |110> -0.25 |111>)\) \(+ (0.25 |000> + 0.25 |001> + 0.25 |010> + 0.25 |011> + 0.25 |100> + 0.25 |101> – 0.75 |110> + 0.25 |111>)\) \(+ (0.25 |000> + 0.25 |001> + 0.25 |010> + 0.25 |011> + 0.25 |100> + 0.25 |101> + 0.25 |110> – 0.75 |111>))\) \( = \frac{1}{2\sqrt{2}} (0.5 |000> + 0.5 |001> + 0.5 |010> + 0.5 |011> + 0.5 |100> + 2.5 |101> + 0.5 |110> + 0.5 |111>) \) \(= 0.18 |000> + 0.18 |001> + 0.18 |010> + 0.18 |011> + 0.18 |100> + 0.88 |101> + 0.18 |110> + 0.18 |111>\)The corresponding probability distribution upon measurement would be
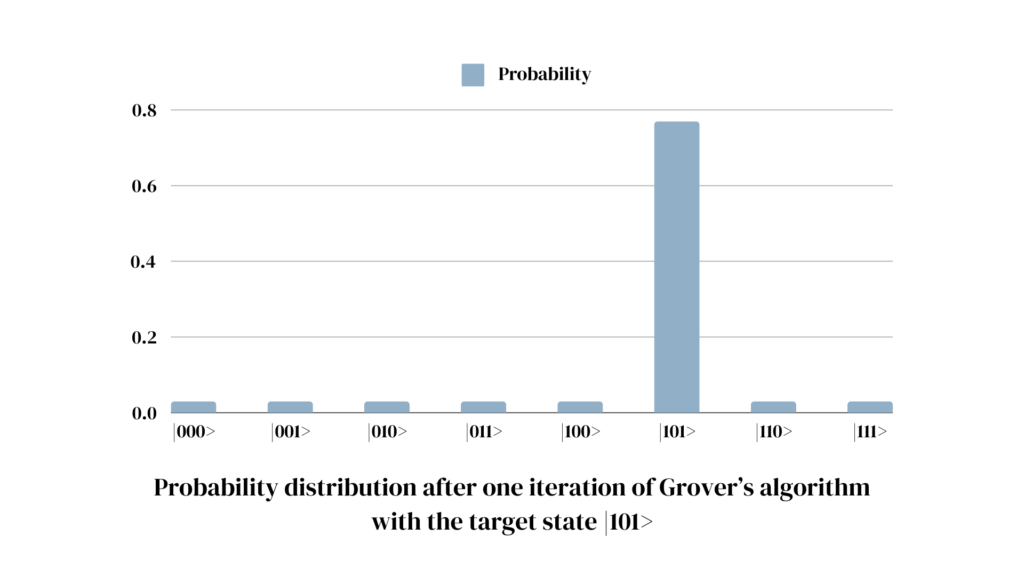
By applying the Oracle and Diffusion Operator once, the probability of the target state |101> has been amplified from 0.125 to 0.77.
What can we learn from Grover’s Algorithm?
While Grover’s Algorithm bears the potential to speed up solution search on a wide range of problems (once quantum hardware catches up), it also illustrates some of the challenges and hurdles in quantum algorithm development.
As explained in the section on the algorithm’s oracle, superposition enables Quantum Parallelism. Since a superposition state comprising multiple base states is itself a valid state, a single operation applied to a system in superposition can affect multiple component states at once. This enabled us to mark the target state among all possibilities in a single operation.
On the other hand, however, since quantum operators have to be unitary matrices, we cannot simply return the state we have identified. The corresponding operation would not be unitary. On a general note, for everything we wish to do in a quantum computer, we must find a way to do it using unitary operators.
Given a quantum oracle function, Grover’s Algorithm provides a way to speed up database search. It does, however, not tell us how to construct such an oracle for new (non-trivial) problems. How to apply the algorithm to a relevant problem and, therefore, compose such an oracle function using the gate set available in a specific quantum computer is in many cases a research domain of its own.
Summary
More than 25 years after its inception, Grover’s Algorithm is still one of the most influential quantum algorithms with a strong potential for near-term application. Through a combination of an oracle function and a custom operator, the algorithm can find a desired solution among all possible alternatives in \(\sqrt{N}\) steps. On a conceptual level, Grover’s Algorithm can be seen as a case study for both the potential and the limitations of quantum computing.