How does Deutsch’s Algorithm work?
In 1985, David Deutsch devised an algorithm to illustrate a situation in which a quantum computer can outperform any classical computer in the amount of required (quantum) oracle calls. While the algorithm itself shows little real-world applicability, it serves as a fascinating case study illustrating the potential of quantum computing in general as well as the quantum oracles formalism and Phase Kickback in particular.
This article covers the basics of Deutsch’s Algorithm: The problem it was originally devised to solve, the structure of its solution, and the practical findings we can derive from it.
The Problem
Some quantum algorithms, such as Grover’s Algorithm, apply to a vast set of problems with real-world implications. Deutsch’s Algorithm, however, is not one of them. It was devised to showcase the advantage quantum computing can hold over classical computing using a contrived problem and a simple yet illustrative quantum circuit.
For the problem, we are presented with a black-box function (aka. the oracle) that receives a single (qu)bit as input and produces a corresponding output through one of two ways: Either, the function always returns the same value (f(0) = 0 and f(1) = 0 or f(0) = 1 and f(1) = 1), or it alternates depending on the input value (f(0) = 0 and f(1) = 1 or f(0) = 1 and f(1) = 0). The goal of Deutsch’s Algorithm is to find out which of the two categories the function belongs to with as few function calls as possible.
In contrast: The best a classical (non-quantum) computer can do is test both possible input values. If the function returns the same value for both inputs, it belongs to the constant category. If output values differ, it’s alternating. With a quantum computer, as Deutsch showed, the same task can be accomplished in a single black-box function call.
The Solution
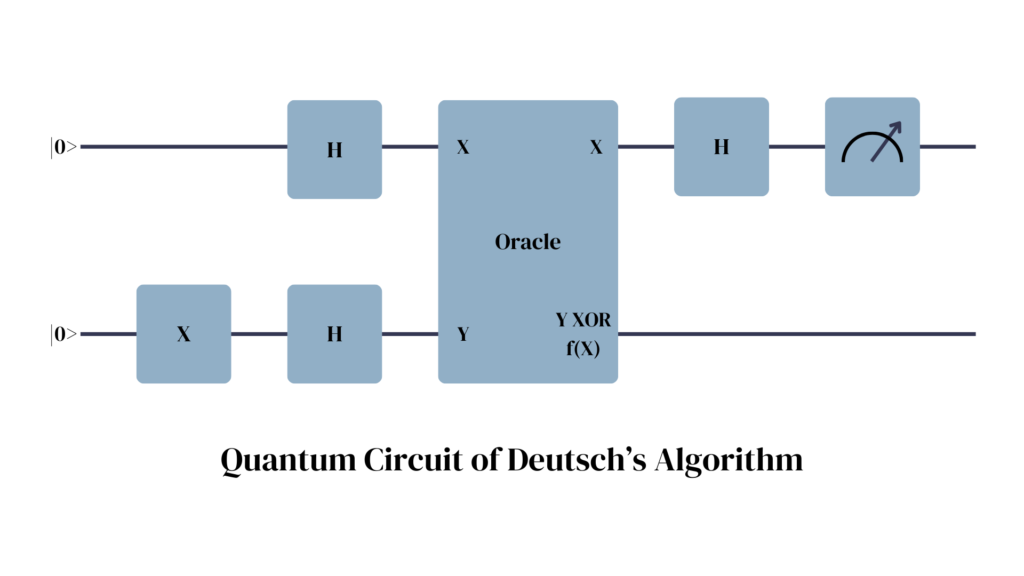
The circuit of Deutsch’s Algorithm consists of two qubits. One qubit indicates the function’s type while the other qubit acts as an ancillary qubit. The indicator qubit is prepared in a state of |+> through a Hadamard gate, while the ancillary qubit is prepared in a superposition state of |->. Then the oracle is applied.
While the oracle does not directly alter the indicator qubit, it applies an XOR operation to the ancillary qubit based on the function value of x. The following calculations illustrate the state of the system after the oracle has been applied, for each of the possible function definitions:
- \(f(x) = 0\) (constant)
$$ U \frac{1}{2} (|00> – |01> + |10> – |11>)$$
$$ = \frac{1}{2} (|00> – |01> + |10> – |11>)$$
$$ = |+->$$
- \(f(x) = 1\) (constant)
$$ U \frac{1}{2} (|00> – |01> + |10> – |11>)$$
$$ = \frac{1}{2} (|01> – |00> + |11> – |10>)$$
$$ = – \frac{1}{2} (- |01> + |00> – |11> + |10>)$$
$$ = – |+->$$
- \(f(0) = 1\) and \(f(1) = 0\) (alternating)
$$ U \frac{1}{2} (|00> – |01> + |10> – |11>) $$
$$ = \frac{1}{2} (|01> – |00> + |10> – |11>) $$
$$ = – \frac{1}{2} (|00> – |01> – |10> + |11>) $$
$$ = – |- -> $$
- \(f(0) = 0\) and \(f(1) = 1\) (alternating)
$$ U \frac{1}{2} (|00> – |01> + |10> – |11>) $$
$$ = \frac{1}{2} (|00> – |01> + |11> – |10>) $$
$$ = |- -> $$
For both constant function types, the system is in a state of |+-> once the oracle function has been applied.* For both alternating function types, the state after the oracle operation is |–>.
* We can safely ignore the global phase of -1 for the cases of f(x) = 1 and (f(0) = 1 and f(1) = 0), since global phase values affect all qubits to the same extent and are lost upon measurement.*
After the application of the final Hadamard gate, the system’s states for each oracle function are:
- \(f(x) = 0\) (constant)
$$(H \otimes I) |+-> = |0->$$
- \(f(x) = 1\) (constant)
$$ -1 \times (H \otimes I) |+-> = -1 \times |0->$$
- \(f(0) = 1\) and \(f(1) = 0\) (alternating)
$$ -1 \times (H \otimes I) |- -> = -1 \times |1->$$
- \(f(0) = 0\) and \(f(1) = 1\) (alternating)
$$ (H \otimes I) |- -> = |1->$$
For both constant oracle functions, the first qubit, earlier referred to as the indicator qubit, is in a state of 0 upon measurement. In the case of both alternating oracle functions, the first qubit is respectively in a state of 1. Since both variants of each function type behave in the same way, a single oracle call can be used to determine which category a given oracle belongs to.
Why does it work?
Although the quantum oracle shown above leaves the indicator qubit unaltered and only acts upon the second qubit, only the first qubit is used to determine which category the embedded oracle function belongs to. This phenomenon as well as the algorithm in general can be explained using the concept of Phase Kickback.
If you are new to Phase Kickback or are interested in its mathematical basis, feel free to have a look at my previous article: What is Phase Kickback?
Phase Kickback occurs whenever a controlled operation is applied from a control qubit in superposition onto a target qubit in one of the eigenstates of the operation. In this case, the target qubit’s state remains unchanged while the corresponding eigenvalue is distributed to the 1 state of the control qubit’s superposition state as relative phase.
If the target qubit is not in one of the eigenstates of the operator, it is changed by the operator as usual. The control qubit remains unaffected.
In our case, the eigenstates of both alternating function definitions are the states |+> and |-> with the corresponding eigenvalues of 1 and -1.
Since the ancillary qubit is in a state of |-> at the beginning of the circuit if the function embedded in the oracle is of the alternating type, the eigenvalue of -1 is “kicked back” to the |1>-state of the control qubit. The qubit’s state is changed from \(\frac{|0> + |1>}{\sqrt{2}} = |+>\) to \(\frac{|0> – |1>}{\sqrt{2}} = |-> \). If the function is of one of the constant types, |-> is not an eigenstate of the operator and the control qubit remains unaffected.
What can we learn from Deutsch’s Algorithm?
Deutsch’s Algorithm works because we can distinguish different function types based on their behavior, even if we do not have any insights into how a given oracle function is implemented. The fact that both alternating function types have the same eigenstate and that this eigenstate is different from the states of both constant function types, enables us to treat both possibilities as one and use Phase Kickback to distribute knowledge about the operator to its control qubit. We do not need full information on the function’s implementation to categorize it.
On a more general notice: Deutsch’s Algorithm shows how Phase Kickback can be used to derive information about any operator, an idea heavily exploited in the Quantum Phase Estimation algorithm.
Summary
Deutsch’s Algorithm was one of the first quantum algorithms to showcase a provable quantum advantage over the best classical algorithm on the same problem. Although the problem Deutsch’s Algorithm solves bears little practical application, the algorithm nicely illustrates how Phase Kickback can be used to extract information about an otherwise opaque operator.