Entanglement and Superposition are the basis of what makes quantum computers different from classical computers and causes their incredible performance gains. In this article, you will learn in a jargon-free way what entanglement is and where it comes from.
What is Entanglement?
Let’s imagine for a second that you have recently decided to open a kindergarten. Since your kindergarten is new, there are only two children enrolled so far. On any given day, each of these children can either be in a good mood 😇 or in a bad mood 😈.
At the beginning of the year, the two children don’t know each other yet, so their moods are independent of one another. For simplicity, let’s assume that each child is in a good mood 50% of the time, and in a bad mood the rest of the time, so also 50%. Whenever you leave the room, thereby unable to observe the children directly, their combined moods are represented in the following probability distribution:
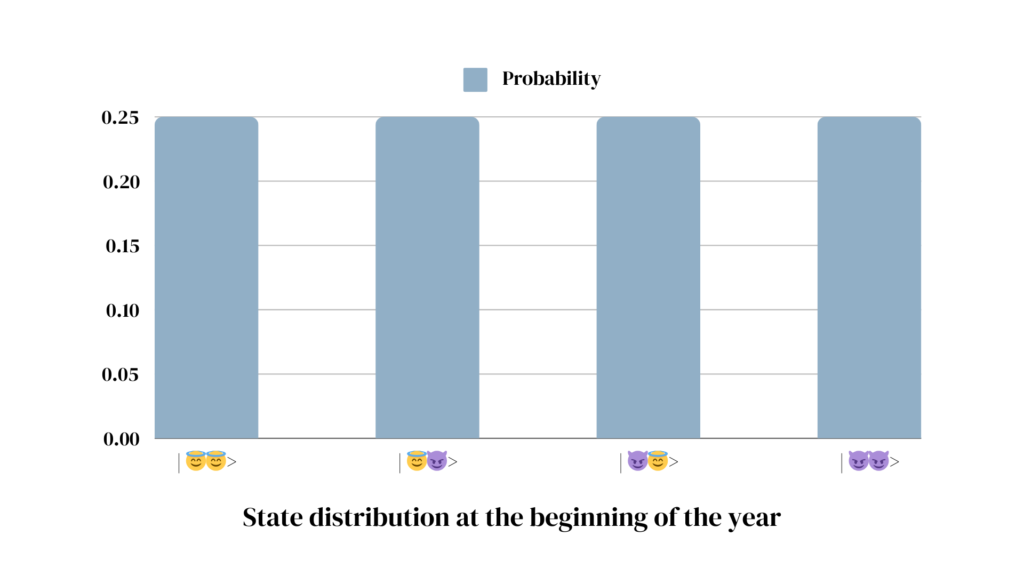
As you get back into the room, you are met with each of the possible mood combinations (|😇😇>, |😇😈>, |😈😇>, |😈😈>)* in roughly 25% of the time. In one out of four cases, you will encounter each of the mood pairings. If you observe the mood of one child first, for example, because they come to meet you at the door, this tells you nothing about the mood of the other child. Their moods are independent of one another.
* Here, we use the braket notation to represent the state of a system (kindergarten), mostly for the sake of consistency with other articles. Do not be concerned with the ins and outs of the notation itself. For now, the only thing that matters is that the braket notation allows us to describe the state of a system of multiple particles in an ordered manner.
After a few days, the two children in your kindergarten become good friends, so their moods begin to align. Whenever one of them is in a good mood, the other child also behaves well and is happy. If one of them is in a bad mood, the other one also starts to act up and behave badly. Now, the new probability distribution of their mood combinations looks as follows:
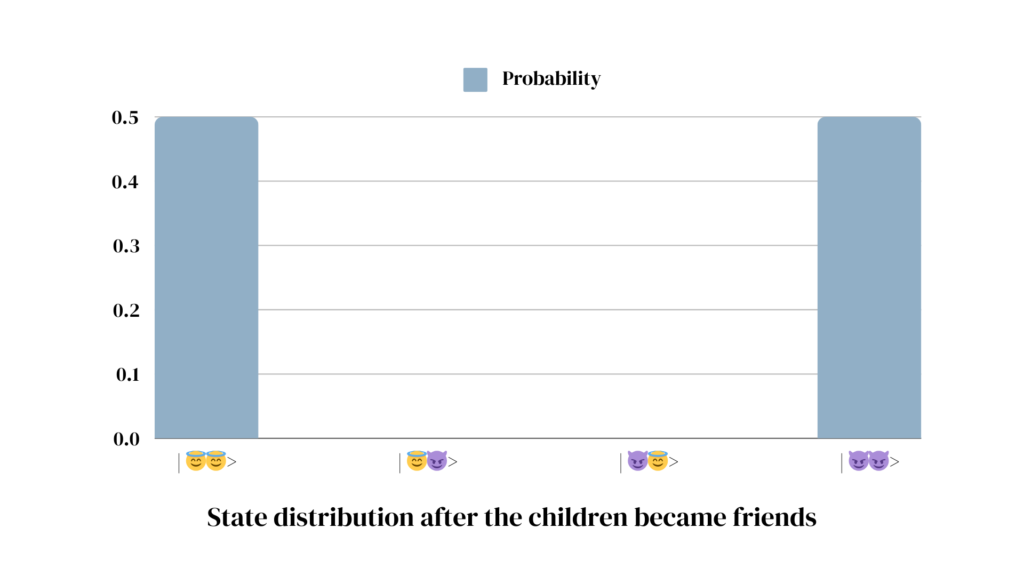
From the previous 4 mood combinations, only two remain in the new setting. Either both children are in a good mood, which happens roughly 50% of the time, or both are in a bad mood. If you know the mood of one of the children, you automatically know the mood of the second one. The moods of both children cannot be described independently from one another anymore, in other words: they have become entangled.
What is entanglement in quantum physics?
In the context of quantum physics, entanglement exists if the states of two particles cannot be described independently from each other, similar to the moods of befriended children in our kindergarten earlier on.
Let’s take the spin direction of an electron as an example.
In simplified terms, an electron can spin either upwards or downwards. Like other quantum particles, the electron can therefore be in a state of either |↑> or |↓> as well as in a superposition of both. A system of two electrons can therefore be measured in one of the following four state combinations: |↑↑>, |↑↓>, |↓↑>, |↓↓>.
Similar to the mood combinations in our kindergarten example, a system of two independent electrons can be represented as the following probability distribution:
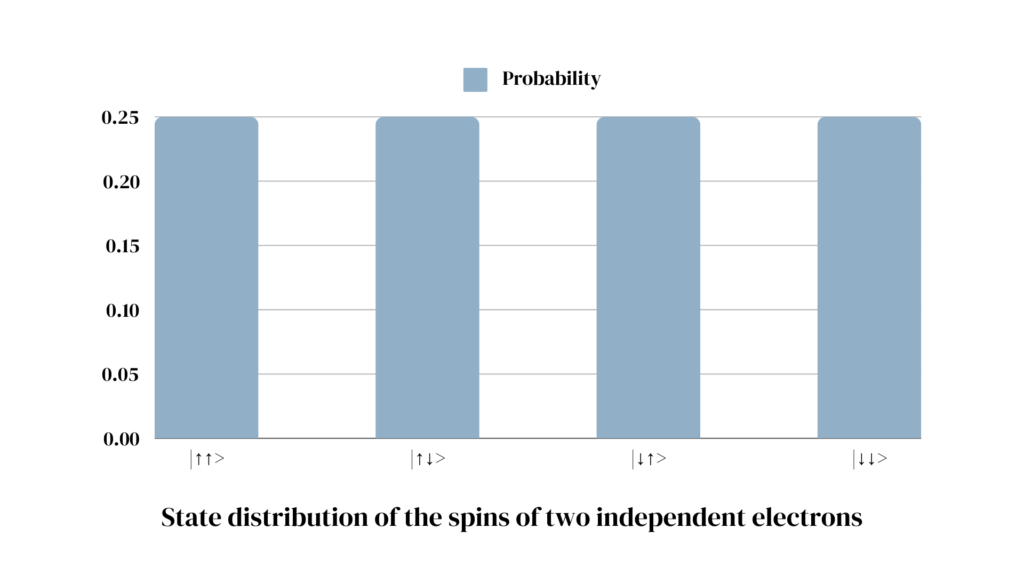
When observed, each of the four state combinations will occur in roughly 25% of all cases. Since the electrons are independent of one another, observing the state of one electron tells us nothing about the state of the other electron. The probability distribution of the combined state can be generated by combining the probability distributions of each independent particle.
In alignment with the children in our kindergarten who became friends: If two particles become entangled, their combined state can no longer be described by looking at each particle in isolation. In the case of electron spins, the probability distribution of an entangled system might look like this:
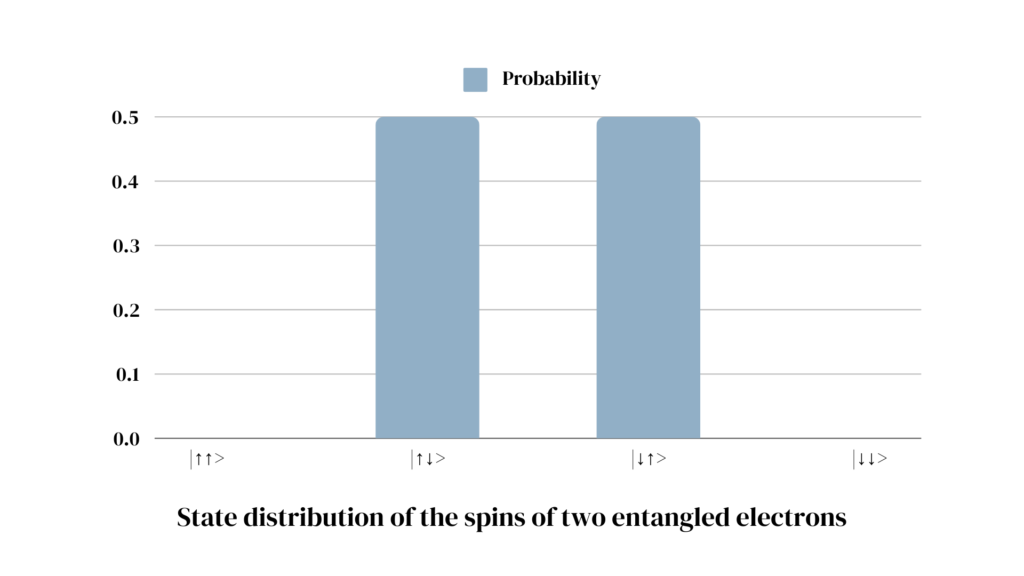
No matter what state we observe the first electron to be in, the second one will be in the opposite state of the first. The combined state is measured as |↑↓> in 50% of all cases and |↓↑> in the rest. If we measure the first electron, we automatically know the state of the second electron when measured.
In contrast to our kindergarten example, however, the entanglement relationship between our electrons also holds if we place our electrons at separate ends of the universe. Once entangled, our electrons cannot be described independently from each other anymore. Their combined probability distribution limits which of the possible combinations we can measure, even if we measure them millions of light years apart. Through entanglement, certain state combinations, such as |↑↑> and |↓↓>, have become impossible. Upon measurement, they will be encountered in 0% of all cases.
Summary
Entanglement is a core concept in quantum computing and one of the reasons why quantum computers can outperform classical computers on certain problems. It occurs, whenever the states of the individual parts of a system cannot be described independently from one other.